Bernoulli's Principle

 Bernoulli's equation is a simple but incredibly important in physics and engineering that can help us understand a lot about the flow of fluids in the world around us. It essentially describes the relationship between the pressure, velocity and elevation of a flowing fluid.

    It has countless applications. We can use it to explain how planes generate lift, or to calculate how fast liquid will drain from a container, for example. We will explore these applications and a few more later on. But let’s start by reviewing the equation itself.

It was first published by the swiss physicist denial Bernoulli in 1738, and it looks like this

The equation states that the sum of these three terms remains constant along a streamline.

    Each of the term is a pressure. The first term is the static pressure, which is just the pressure P of the fluid. Then we have the dynamic pressure which is the function of the fluid density ρ(Rho) and velocity V, and represents the fluid kinetic energy per unit volume.

    And the last term is the hydrostatic pressure which is the pressure exerted by the fluid due to gravity. g is the gravitational acceleration and h is the elevation of the fluid, which is just its height above a reference level.

    This is the pressure form of the equation, but it can also be represented in the head form and energy form.

    We can think of Bernoulli’s equation as the statement of the conservation of the energy. It says that along a stream line the sum of the pressure energy, kinetic energy and potential energy remains constant. This is really valuable information that can help us analyze a whole range of fluid flow problems.

    The equation does have a few limitations which will we covered later in the article, but for now the important thing to note is that it can only be applied along a streamline.

 

    We can define a streamline in steady flow as the path traced by a single particle within the fluid. or more technically as a curve that at all points is tangent to the particle velocity vector.

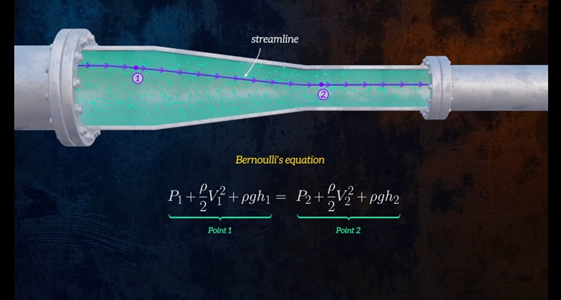
    Lets look at an example where we apply Bernoulli’s equation to flow through a pipe which has a change in diameter. We want to use the equation to see how the pressure changes as the flow passes from the larger to the smaller diameter. Bernoulli’s equation is usually used to compare the flow at two different locations so we can rewrite it like

With point 1 & 2 both being on the same streamline.

    There is no significant change in elevation between points 1 & 2, so potential energy terms cancel other out. And if we put all of the static pressure terms on the side, we get this equation for change in pressure.

    If we assume that the fluid is incompressible, the mass flow rates at point 1 & 2 must be equal. This gives us what called the continuity equation, which is just a statement of conservation of mass.

    Mass flow rate is equal to the product of the fluid density, the pipe cross sectional area and the fluid velocity.

    So, we can re-arrange the continuity equation to obtain an equation for the velocity at point 2.

    The cross-sectional area A₂ is smaller than A₁, which means that the velocity of the flow increases as it passes into the smaller diameter pipe. This is quite intuitive. By substituting this value for V₂ into Bernoulli’s equation, we can see that since the velocity increases between points 1 & 2, pressure between both points must decreases.

    This concept, that for horizontal flow an increase in fluid velocity must be accompanied by a decrease in pressure, is one way of formulating what we call Bernoulli’s principle. It can seem counter-intuitive, because people often expect an increase in velocity to result in a corresponding increase in pressure. But it makes sense if we think about the conservation of energy. The energy required to increase the fluid velocity comes at the expense of the static pressure energy. Bernoulli’s principle shows up in a lot of different places.

Telegram channel- Join Now

Applications area of Bernoulli's equation

    # We can use it to help explain how plane wings generates lift. Fluid flowing over an air foil travels faster than fluid flowing below it.

    According to Bernoulli’s principle this creates an area of low pressure above the airfoil and area of high pressure below it, and it’s, this pressure difference that generates lift.

    # Bernoulli’s principle also explains how Bunsen burners works. When the gas valve is opened, gas flows into the barrel at high velocity. Following Bernoulli’s principle, this high velocity creates an area of low pressure in the barrel, which draws air in through the air regulator, allowing for more complete combustion of the gas.

    # Several different flow measurement devices rely on Bernoulli’s equation to determine the velocity of a flowing fluid. The pitot static tube is one such device. It’s often used in aircraft to measure air speed

    # another flow measurement device that uses Bernoulli’s principle is venturimeter, which is an instrument used to determine the flowrate through a pipe. It works by measuring the pressuring drop across a converging section of the pipe. 

     Say we want to determine the flow rate Q, which is the velocity multiplied by the pipe cross sectional area at point 1. We can easily re-arrange the pressure drop equation we derived earlier when we looked at change in diameter, to get this equation for flow rate. All we need to know is the dimension of the venturimeter, the fluid density and the pressure P₁ and P₂, and that allows us to calculate the flow rate. The venturimeter has no moving parts and is a very simple and reliable way of measuring the flowrate through a pipe. The diverging section is longer than the converging section to reduce the likehood of flow separation and keep energy losses low.

    # let’s look at one more example where we can apply Bernoulli’s equation. Say we have a beer keg, and we want to calculate how fast will draw when we first open the tap at the bottom. All we need to do is define our two points along a stream line and apply Bernoulli’s equation. It is a gravity-fed keg with a went at the top, meaning that it’s not pressurised. The pressure at both points will be atmospheric, and so that static pressure terms cancel each other out.

@@9*7

    We can also assume the keg is large enough that the fluid velocity at point 1 is close to zero. If we re-arrange the Bernoulli’s equation, and define the height between the beer level and the tap as h, we get this equation for the beer velocity out the tap.

    Those were a few examples of cases where we can apply Bernoulli’s equation to get some valuable information or to solve a problem. But to use it correctly, it’s important to have an understanding of the limitations of the equation which arise because how it’s derived.

Limitations

    There are several different ways Bernoulli’s equation can be derived. It can be derived based on conservation of energy, by considering that the work done on the fluid increases its kinetic energy. Or it can be derived by applying Newton’s second law, which involves determining the forces acting on a fluid particle and applying 

    They do both make some assumption that we need to be aware of, since they limit how we can apply the equation.

    Firstly, the derivation of Bernoulli’s equation assumes that flow is laminar and that it is steady, meaning that it does not vary with time. Next, it assumes that the flow is inviscid, meaning that shear forces due to fluid viscosity are negligible. This assumption is needed because viscosity would result in a dissipation of some of the fluids internal energy, and so the idea that energy is conserved along a streamline will no longer apply. And finally, the derivation of Bernoulli’s equation assumes that the fluid behaves as if it’s incompressible. This is usually valid for liquids, but might not be for gases at high velocities. All three of these assumptions need to be valid if we want to apply Bernoulli’s equation. Adapted versions of the equation which can be applied to unsteady and compressible flows do not exist. Although they are a bit more complicated.

Conclusion

    Being able to recognise when Bernoulli’s principle is at play or when Bernoulli’s equation can be applied to solve a problem is a powerful tool in any engineer’s arsenal. 

Reference- The efficient engineering

Telegram channel- Join Now